衡水金卷 2022-2023学年度上学期高一年级期中考试·月考卷 英语(人教版)试题答案

衡水金卷 2022-2023学年度上学期高一年级期中考试·月考卷 英语(人教版)试题答案，目前我们已经整理了衡水金卷 2022-2023学年度上学期高一年级期中考试·月考卷 英语(人教版)试题答案的各科答案和试卷，更多全国名校联考答案，请关注本网站。

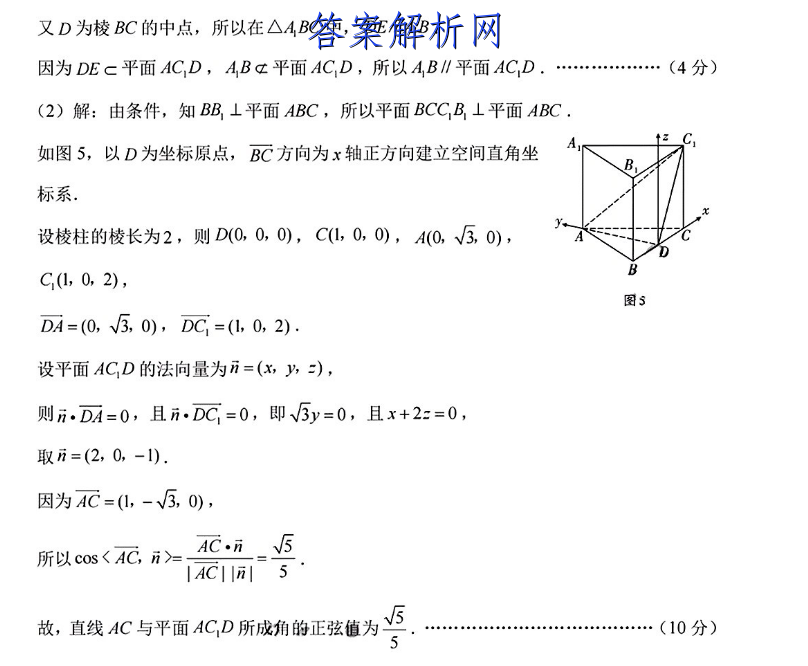
四、解答题（共70分.解答应写出文字说明，证明过程或演算步骤）17.(本小题满分10分)(1)证明：如图4，连接AC,与AC,相交于点E,连接DE.则在平行四边形ACC,A中，E为AC的中点.B又D为棱BC的中点，所以在△ABC中，DE∥A,B.因为DEc平面ACD,A,B文平面ACD,所以AB∥平面AC,D.…(4分)(2)解：由条件，知BB⊥平面ABC,所以平面BCCB⊥平面ABC.如图5，以D为坐标原点，BC方向为x轴正方向建立空间直角坐标系设棱柱的棱长为2，则D(0,0,0),C(1,0,0),A0,√3,0)，C(1,02),图3DA=(0,V3,0),DC=(1,0,2).设平面ACD的法向量为方=(x,y,),则i.DA=0,且i.DC=0,即√5y=0,且x+2:=0,取n=(2,0,-1).因为AC=(1,-V3,0),所以cos〈AC,i>AC.n5IACI5故，直线4C与平面ACD所成角的正弦值为5…(10分)

16,由-=g+小+x=le(x=le,4+小-x=国，知f为偏质数。当x≥0时，=4≥0知，)在0，+0)上单调递增且f)≥0，设4+1g(x)=f(x),则g(x对为奇函数且在[0，+∞)上单调递增，结合奇函数的对称性可得g(x)在(-o,+∞)单调递增，由题得g(a)+g(a)+g(a)+g(a)=0,又{an}是等差数列，可得4+a=a2+a3,当41+a4>0时，a4>-a4=g(a)>g(-a4)=g(a)>-g(a4)三g(a)+ga,)>0,同理g(a2)+g(a)>0,即g(a)+g(a)+g(a)+g(a)>0,不合题意，当a+a<0时，同理可得g(4,)+g(a2)+g(a)+g(a,)<0,也不合题意；所以a+a4=0,又公差为4，可得a=-6,所以S.=m×(-6)+m”,-》x4=2n2-8m.2