衡水金卷先享题分科综合卷 新教材2023理综一 答案

衡水金卷先享题分科综合卷 新教材2023理综一 答案，目前衡水金卷先享题网已经汇总了衡水金卷先享题分科综合卷 新教材2023理综一 答案的各科答案和试卷，更多衡水金卷答案请关注本网站。

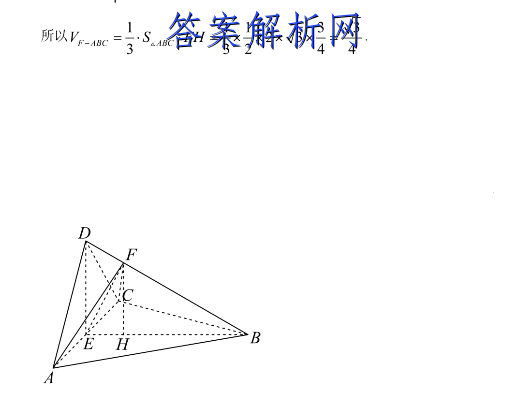
【答案】1)证明详见解析4【解析】【分析】(1)通过证明AC⊥平面BED来证得平面BED⊥平面ACD(2)首先判断出三角形AFC的面积最小时F点的位置，然后求得F到平面ABC的距离，从而求得三棱锥F-ABC的体积，【小问1详解】由于AD=CD,E是AC的中点，所以AC⊥DE.AD=CD由于{BD=BD,所以△ADB兰△CDB,∠ADB=∠CDB所以AB=CB,故AC⊥BD,由于DE O BD=D,DE,BDI平面BED,所以AC⊥平面BED,由于ACc平面ACD,所以平面BED⊥平面ACD【小问2详解】依题意AB=BD=BC=2,∠ACB=6O°，三角形ABC是等边三角形，所以AC-2,AE=CE=1,BE=5,由于AD=CD,AD⊥CD,所以三角形ACD是等腰直角三角形，所以DE=I,DE2+BE2=BD2,所以DE⊥BE,由于ACn BE=E,AC,BEC平面ABC,所以DE⊥平面ABC.由于△ADB兰△CDB,所以∠FBA=∠FBC,BF BE由于∠FBA=∠FBC,所以△FBA=AFBC,AB=CB所以AF=CF,所以EF⊥AC,由于Sc=2·1C,EF,所以当EF最短时，三角形AC的面积最小值过E作EF⊥BD,垂足为F,在Rt△BED中，BEDE=D-EF,解得EF=28F2-DF-3所以BF 3BD 4.所以写8chH-写**2xv5x-53244DEHBA

【答案】1)5π(2)证明见解析【解析】【分析】(1)根据题意可得，sinC=sin(C-A),冉结合三角形内角和定理即可解出：(2)由题意利用两角差的正弦公式展开得sinC(sin Acos B-cos Asin B)=sinB(sin Ccos A-cos Csin A),再根据正弦定理，余弦定理化简即可证出.【小问1详解】由A=2.s血Csn(A-B)=sBsn(C-4可，得sinCsin=n8s如(C-A利.面0

0,而0